







---> Themen <---
In diesem Tutorial kann ein neuronales Netzwerk direkt im Browser trainiert werden. Dabei werden Aufbau und Funktionsweise eines neuronalen Netzwerks als Grundlage von KI Modellen beschrieben und Neuronen sowie Schichten als wesentliche Grundbegriffe neuronaler Netzwerke vorgestellt. Ergänzend werden die Anzahl an Epochen und die dazugehörige Lernrate als sogenannte Hyperparameter eingeführt, welche den Trainingsprozess von KI Modellen maßgeblich mitbestimmen können. Über den Trainingsprozess des neuronalen Netzwerks kann schließlich das Konzept der Aktivierungsfunktionen verdeutlicht werden, die bestimmen, wie die gelernten Parameter als Weights und Biases in Ausgaben umgewandelt werden. Sind diese transparent ausgewiesen, können KI Modelle bedarfsspezifisch angepasst und optimiert werden. Die Modellgenauigkeit kann sodann über die Konfusionsmatrix und die daraus resultierende Genauigkeit bewertet werden. Ein Einblick in die False Negatives und False Positives ermöglicht abschließend eine datenbasierte Einzelfallbetrachtung, um den Trainingsprozess, die Qualität der verwendeten Daten und die Qualität des KI Modells bewerten zu können.
---> Ziele <---
Insgesamt stehen die wesentlichen Grundbegriffe neuronaler Netzwerke, eine vereinfachte Darstellung der mathematischen Grundlagen, als auch die daraus resultierende Interpretierbarkeit der Ergebnisse sowie die Möglichkeiten zur Optimierung im Fokus des Tutorials. Übergreifendes Ziel des Tutorials ist eine transparente Ausweisung der Funktionsweise neuronaler Netzwerke für ein besseres Verständnis von KI Modellen.

---> Datensatz <---
Das Tutorial basiert auf einem Datensatz (Download: CSV) zur Klassifikation von Schwertlilienarten, mit Angaben zu Länge und Breite von Kelchblatt und Kronblatt. In dem Datensatz sind insgesamt vier unabhängige Variablen enthalten, welche zur Klassifikation der Schwertlilien herangezogen werden können. Ergänzend ist eine abhängige Variable enthalten, welche Auskunft darüber gibt, um welche Schwertlilienart es sich handelt. Es handelt sich demnach um bereits bekannte Fälle, auf deren Grundlage das neuronale Netzwerk die (komplexen) Muster erlernen soll, die den Schwertlilienarten zugrundeliegen können, um diese korrekt klassifizieren zu können. Dies setzt allerdings voraus, dass zukünftige Fälle ähnliche Muster aufweisen wie die zum Training des neuronalen Netzwerks verwendeten Fälle.
---> Variablen <---
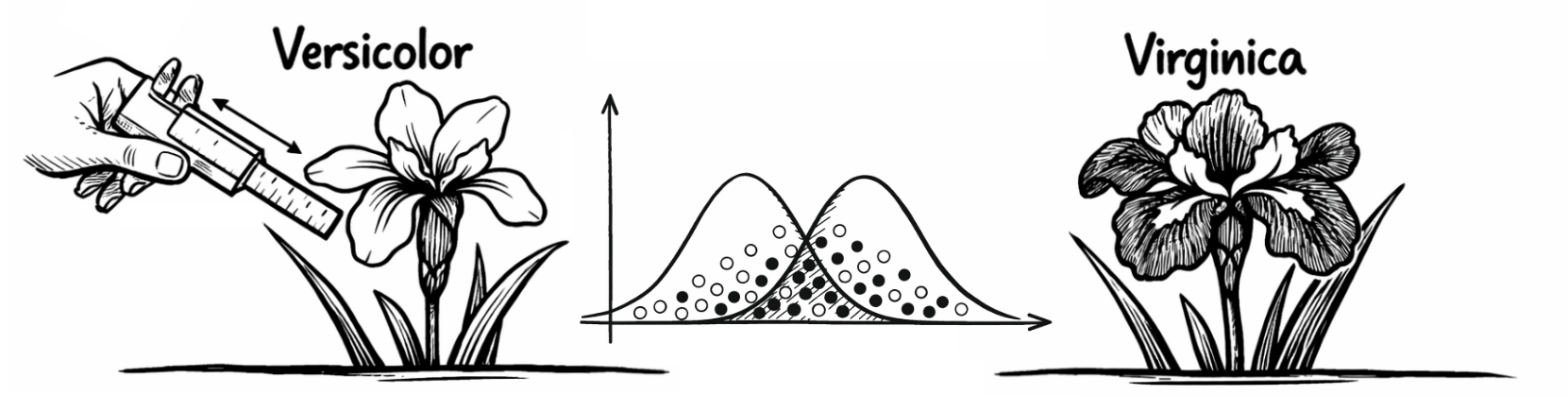
Die unabhängigen Variablen lauten: (1) Länge des Kelchblatts (cm), (2) Breite des Kelchblatts (cm), (3) Länge des Kronblatts (cm) sowie (4) Breite des Kronblatts (cm). Die Ähnlichkeit der unabhängigen Variablen erschwert jedoch die Klassifizierung. Die abhängige Variable beinhaltet entsprechend die Merkmale 0 für "Versicolor" und 1 für "Virginica" für die zugrundeliegenden Schwertlilienarten. Die Variablen sind gleich skaliert und erfordern keine weitere Standardisierung.

---> Neuronen <---
Neuronen in einem neuronalen Netzwerk sind grundlegende Bausteine, die Informationen verarbeiten können. Sie erhalten eine Eingabe, verarbeiten diese und erzeugen dann eine entsprechende Ausgabe. Neuronen können mit anderen Neuronen verbunden sein, d.h. die Eingabe eines Neurons basiert in der Regel auf der Ausgabe eines anderen Neurons. Bei dem standardmäßig angezeigten kleinen neuronalen Netzwerk werden zunächst 11 Neuronen über alle Schichten hinweg dargestellt, beim größeren neuronalen Netzwerk sind es 17 Neuronen über alle Schichten hinweg.
---> Schichten <---
Die Schichten in einem neuronalen Netzwerk sind Gruppen von Neuronen, die zusammenarbeiten, um Eingabedaten zu verarbeiten und gemeinsam eine Ausgabe zu erzeugen. Dabei ist das Zusammenspiel aus Eingabeschicht als erste Schicht des neuronalen Netzwerks zur Dateneingabe, den verborgenen Schichten, die zwischen der Eingabeschicht und der Ausgabeschicht komplexe Muster erkennen können und der Ausgabeschicht, welche als letzte Schicht des neuronalen Netzwerks die Antwort eines KI Modells ausgibt, entscheidend. Das standardmäßig angezeigte kleine neuronale Netzwerk basiert auf 4 Schichten, das größere neuronale Netzwerk basiert hingegen auf 5 Schichten. Ein Klick auf den Button "Training starten" trainiert das neuronale Netzwerk und ermöglicht nachfolgend einen Einblick in die verwendeten Aktivierungsfunktionen, Parameter und die Modellgenauigkeit:
---> Epochen <---
Epochen sind vollständige Durchgänge aller Daten, die für den Trainingsprozess verwendet werden. Bei den vorliegenden Daten bedeutet dies, dass das neuronale Netzwerk jeden Fall aus den Daten einmal gesehen und verarbeitet hat. Ein neuronales Netzwerk benötigt in der Regel mehrere Epochen, um komplexe Muster erkennen zu können. Entsprechend umsichtig ist dieser sogenannte Hyperparameter zu wählen. Wenn das neuronale Netzwerk nur eine geringe Anzahl an Epochen durchläuft, hat es vielleicht nicht genug Zeit, die komplexen Muster in den Daten zu erkennen (Stichwort: Underfitting). Wenn das neuronale Netzwerk zu viele Epochen aufweist, kann es anfangen, die Trainingsdaten so gut zu lernen, dass eine hohe Passung zu den Daten aus dem Trainingsprozess gegeben ist, diese Passung aber nicht auf weitere Daten übertragen werden kann (Stichwort: Overfitting). Bei dem standardmäßig angezeigten neuronalen Netzwerk sind zunächst 100 Epochen voreingestellt.
---> Lernrate <---
Die Lernrate ist ebenfalls ein Hyperparameter und beeinflusst, wie schnell oder langsam das neuronale Netzwerk aus seinen Fehlern lernt. Sie steuert die Größe der Schritte, die das Netzwerk bei der Anpassung der Gewichte während des Trainingsprozesses macht. Eine zu hohe Lernrate kann dazu führen, dass das Modell die optimale Lösung überspringt, während eine zu niedrige Lernrate das Training sehr langsam und ineffizient machen kann. Die beim standardmäßig angezeigten neuronalen Netzwerk voreingestellte Lernrate beträgt 0.05 und kann entsprechend angepasst werden.

---> Aktivierungsfunktionen <---
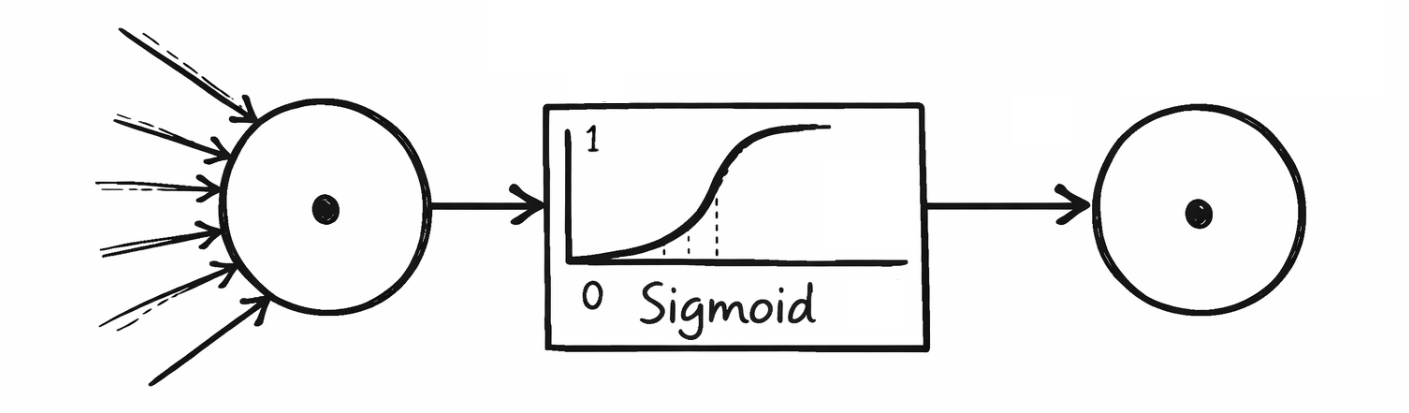
Aktivierungsfunktionen bestimmen, wie stark ein Neuron aktiviert wird und welche Ausgabe es an die nächste Schicht weitergibt. Sie helfen dabei, irrelevante Informationen zu filtern und die relevanten Muster zu verstärken. Häufig verwendete und in den neuronalen Netzwerken des Tutorials hinterlegte Aktivierungsfunktionen sind Sigmoid, Hyperbolischer Tangens, Rectified Linear Unit und Leaky Rectified Linear Unit. Nachfolgend ist ausgewiesen, welche Aktivierungsfunktionen in welchen Schichten zur Anwendung gekommen sind:
---> Mathematischer Hintergrund <---
Sigmoid gibt Werte im Bereich (0, 1) aus und wird oft in der Ausgabeschicht von binären Klassifikatoren verwendet, um bspw. die Wahrscheinlichkeit für 1 "Virginica" zu berechnen.
Hyperbolischer Tangens gibt hingegen Werte im Bereich (-1, 1) aus und verhält sich ähnlich zu Sigmoid, ist jedoch symmetrischer und von Vorteil, wenn die Ausgabe zentriert werden soll.
Rectified Linear Unit ist eine der am häufigsten verwendeten Aktivierungsfunktionen und gibt den Eingabewert direkt zurück, wenn er größer als 0 ist, andernfalls wird 0 ausgegeben. Dies kann allerdings dazu führen, dass Neuronen im Trainingsprozess mittel- bis langfristig ausgeschaltet werden (Stichwort: Dead Neurons). Eine Variante davon ist Leaky Rectified Linear Unit, die für negative Werte eine kleine Neigung zulässt, um auch bei negativen Eingaben eine kleine Aktivierung zuzulassen und so das Problem der Dead Neurons zu reduzieren.

---> Architektur eines neuronalen Netzwerks <---
Das Training eines neuronalen Netzwerks passt die Weights und Biases als Parameter schrittweise an, welche sich in der zugrundeliegenden Architektur des neuronalen Netzwerks ausweisen lassen. Dabei werden die Weights (w) und Biases (b) so angeordnet, wie sie von den jeweiligen Schichten ausgegeben bzw. in die nachfolgenden Schichten eingegeben werden. Die erste verborgene Schicht erhält aus der Eingabeschicht die Eingabewerte der vier unabhängigen Variablen aus den ursprünglichen Daten, weshalb für die Weights vier Spalten in der Architektur des neuronalen Netzwerks vorgesehen sind. Diese vier Spalten stehen stellvertretend für die Anzahl an Neuronen der vorherigen Schicht, also der Eingabeschicht. Die Zeilen stehen stellvertretend für die Anzahl an Neuronen in der aktuellen Schicht, entsprechend sind es im vorliegenden Beispiel vier Neuronen in der ersten verborgenen Schicht. Die vier Neuronen geben nicht nur ihre Weights an die nachfolgende Schicht weiter, sondern diese werden zusätzlich um die Biases aus dem Trainingsprozess ergänzt. Das mathematische Verfahren hierbei ist die sogenannte Matrixmultiplikation. In der Ausgabeschicht befindet sich letzlich nur ein Neuron, welches zwischen 0 und 1 für "Versicolor" bzw. "Virginica" klassifizieren kann. Die daraus resultierende Architektur des neuronalen Netzwerks sieht wie folgt aus:
---> Weights <---
Weights bestimmen die Stärke der Verbindung zwischen den Neuronen in benachbarten Schichten des Netzwerks. Ein Gewicht multipliziert die Eingabewerte, bevor sie an das nächste Neuron weitergegeben werden (Stichwort: Matrixmultiplikation). Höhere Gewichtswerte verstärken die Eingabe, niedrigere Werte schwächen sie.
---> Biases <---
Biases sind zusätzliche Werte, die dazu verwendet werden können, das Ergebnis eines Neurons zu verschieben. Dadurch kann das neuronale Netzwerk flexibler lernen und bedarfsspezifisch angepasst werden. Beispiel: Ohne einen entsprechenden Bias könnte ein Neuron immer nur eine Ausgabe von 0 haben, wenn die Eingabewerte ebenfalls 0 sind. Der Bias verhindert das, um die Eingabewerte für den weiteren Trainingsprozess erhalten zu können.

---> Konfusionsmatrix <---
Eine Konfusionsmatrix ist eine Tabelle, die verwendet wird, um die Leistung eines Klassifikationsmodells zu bewerten. Sie zeigt, wie gut das Modell verschiedene Klassen vorhersagt, indem sie die tatsächlichen Werte mit den vorhergesagten Werten vergleicht. Die Matrix besteht in der Regel aus vier Feldern. True Positives (TP): Die Anzahl der richtigen positiven Vorhersagen (das Modell sagt "positiv" und es ist auch "positiv"). False Positives (FP): Die Anzahl der falschen positiven Vorhersagen (das Modell sagt "positiv", aber es ist eigentlich "negativ"). True Negatives (TN): Die Anzahl der richtigen negativen Vorhersagen (das Modell sagt "negativ" und es ist auch "negativ"). False Negatives (FN): Die Anzahl der falschen negativen Vorhersagen (das Modell sagt "negativ", aber es ist eigentlich "positiv"). Auf der Grundlage des trainierten neuronalen Netzwerks ergibt sich folgende Konfusionsmatrix:
---> Genauigkeit <---
Die Genauigkeit (Stichwort: Accuracy) eines neuronalen Netzwerks ist eine der häufigsten Metriken, um die Leistung eines Klassifikationsmodells zu messen. Sie gibt an, wie oft das Modell die richtige Vorhersage getroffen hat. Die Genauigkeit wird berechnet, indem man die Anzahl der korrekten Vorhersagen (sowohl positive als auch negative) durch die Gesamtzahl der Vorhersagen teilt. Die Accuracy ist allerdings nur dann eine geeignete Metrik, wenn keine der Fälle mit den Merkmalsausprägungen 0 oder 1 unter- oder überrepräsentiert ist.

---> Optimierung <---
Abschließend können die False Negatives und False Positives als falsche Vorhersagen des KI Modells im zugrundeliegenden Datensatz betrachtet werden (Download: CSV). Hierbei gilt es herauszufinden, welche Besonderheiten im Einzelfall vorgelegen haben und von den gelernten Mustern des neuronalen Netzwerks abweichen. Dadurch lässt sich ggfls. nicht nur das neuronale Netzwerk durch erneutes Training, veränderte Hyperparameter oder angepasste Daten optimieren, sondern auch ein Verständnis dafür ableiten, welche Limitationen bei den gegebenen Daten unter Verwendung eines neuronalen Netzwerks zu berücksichtigen sind:
---> Abschließende Bemerkungen <---
Die Möglichkeit zur manuellen Optimierung ist außerhalb des Tutorials unter Rückgriff auf eine Programmiersprache wie Python oder MicroPython möglich, um KI Modelle bedarfsspezifisch in den beruflichen Kontext überführen zu können. Das vorliegende Tutorial basiert auf einem Open Source Framework, welche zu diesem Zweck alle Parameter und Hyperparameter eines neuronalen Netzwerks transparent ausweist, um KI Modelle flexibel anpassen und erklärbar gestalten zu können - bspw. auch die Anzahl der Neuronen und Layer sowie die verwendeten Aktivierungsfunktionen, inklusive Export auf einen Microcontroller wie den Raspberry Pi Pico (Link: KI-ENNA). Mit Blick auf die Klassifikation der Schwertlilien ist abschließend festzuhalten, dass solche KI Modelle lediglich als Assistenzsysteme zu verstehen und zu verwenden sind, um bspw. bei einem erhöhten Fallaufkommen Hinweise liefern zu können. Dass die von einem KI Modell gelieferten Hinweise nicht korrekt sein müssen, wurde durch die False Positives und False Negatives verdeutlicht. Die menschliche Expertise und Erfahrung kann dabei nicht durch das KI Modell ersetzt werden.


Prof. Dr. habil. Dennis Klinkhammer
www.STATISTICAL-THINKING.de