







---> Topics <---
In this tutorial, a neural network can be trained directly in the browser. The structure and functioning of a neural network as the basis of AI models are described, and neurons and layers are introduced as essential basic concepts of neural networks. In addition, the number of epochs and the associated learning rate are introduced as so-called hyperparameters, which can significantly influence the training process of AI models. Finally, the training process of the neural network can be used to illustrate the concept of activation functions, which determine how the learned parameters are converted into outputs as weights and biases. If these are transparently identified, AI models can be adapted and optimized to specific requirements. The model accuracy can then be evaluated using the confusion matrix and the resulting accuracy. Finally, an insight into false negatives and false positives enables a data-based case-by-case analysis to evaluate the training process, the quality of the data used, and the quality of the AI model.
---> Goals <---
Overall, the tutorial focuses on the essential basic concepts of neural networks, a simplified presentation of the mathematical fundamentals, the resulting interpretability of the results, and the possibilities for optimization. The overarching goal of the tutorial is to provide a transparent explanation of how neural networks work in order to promote a better understanding of AI models.

---> Dataset <---
The tutorial is based on a dataset (Download: CSV) for classifying iris species, with information on the length and width of the sepals and petals. The dataset contains a total of four independent variables that can be used to classify the irises. In addition, there is a dependent variable that provides information about the iris species in question. These are therefore already known cases, on the basis of which the neural network is to learn the (complex) patterns that may underlie the iris species in order to classify them correctly. However, this presupposes that future cases will exhibit similar patterns to those used to train the neural network.
---> Variables <---
The independent variables are: (1) length of the sepal (cm), (2) width of the sepal (cm), (3) length of the petal (cm), and (4) width of the petal (cm). However, the similarity of the independent variables makes classification difficult. The dependent variable accordingly contains the characteristics 0 for “Versicolor” and 1 for “Virginica” for the underlying iris species. The variables are scaled equally and do not require further standardization.

---> Neurons <---
Neurons in a neural network are basic building blocks that can process information. They receive input, process it, and then generate a corresponding output. Neurons can be connected to other neurons, meaning that the input of one neuron is usually based on the output of another neuron. The small neural network displayed by default initially shows 11 neurons across all layers, while the larger neural network shows 17 neurons across all layers.
---> Layers <---
The layers in a neural network are groups of neurons that work together to process input data and jointly generate an output. The interaction between the input layer as the first layer of the neural network for data input, the hidden layers that can recognize complex patterns between the input layer and the output layer, and the output layer, which as the last layer of the neural network outputs the response of an AI model, is crucial. The small neural network displayed by default is based on 4 layers, while the larger neural network is based on 5 layers. Clicking on the “Start training” button trains the neural network and subsequently provides insight into the activation functions, parameters, and model accuracy used:
---> Epochs <---
Epochs are complete passes through all data used for the training process. With the data at hand, this means that the neural network has seen and processed each case from the data once. A neural network usually needs several epochs to recognize complex patterns. This so-called hyperparameter must therefore be chosen with care. If the neural network only goes through a small number of epochs, it may not have enough time to recognize the complex patterns in the data (keyword: underfitting). If the neural network has too many epochs, it may begin to learn the training data so well that it fits the data from the training process very well, but this fit cannot be transferred to other data (keyword: overfitting). The neural network displayed by default is initially preset to 100 epochs.
---> Learning Rate <---
The learning rate is also a hyperparameter and influences how quickly or slowly the neural network learns from its mistakes. It controls the size of the steps the network takes when adjusting the weights during the training process. A learning rate that is too high can cause the model to skip the optimal solution, while a learning rate that is too low can make training very slow and inefficient. The default learning rate for the neural network displayed by default is 0.05 and can be adjusted accordingly.

---> Activation Functions <---
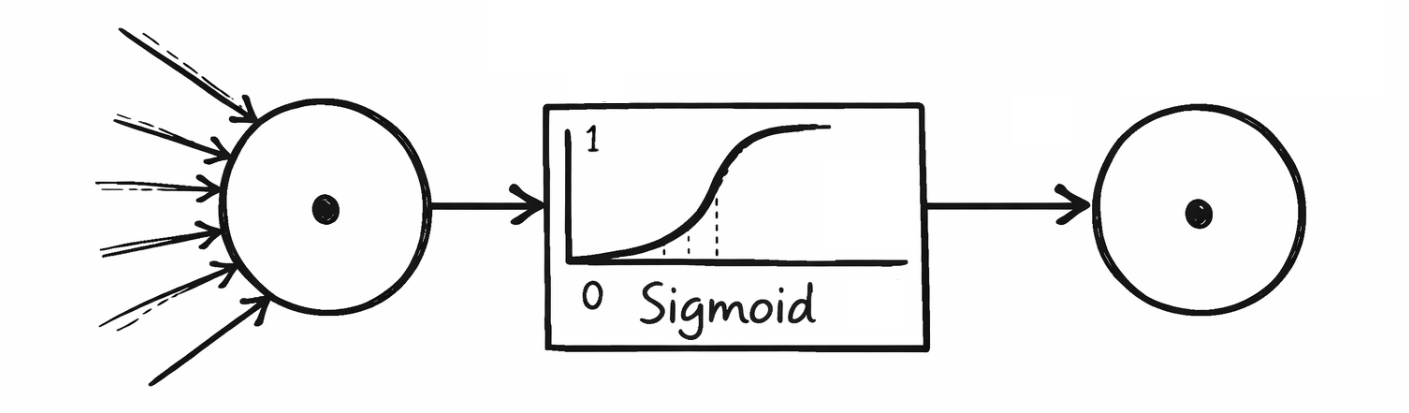
Activation functions determine how strongly a neuron is activated and what output it passes on to the next layer. They help to filter out irrelevant information and reinforce relevant patterns. Frequently used activation functions stored in the neural networks of the tutorial are sigmoid, hyperbolic tangent, rectified linear unit, and leaky rectified linear unit. The following shows which activation functions were used in which layers:
---> Mathematical Background <---
Sigmoid outputs values in the range (0, 1) and is often used in the output layer of binary classifiers to calculate, for example, the probability of 1 “Virginica.” Hyperbolic Tangent, on the other hand, outputs values in the range (-1, 1) and behaves similarly to Sigmoid, but is more symmetrical and advantageous when the output needs to be centered. Rectified Linear Unit is one of the most commonly used activation functions and returns the input value directly if it is greater than 0, otherwise 0 is output. However, this can lead to neurons being switched off in the medium to long term during the training process (keyword: dead neurons). A variant of this is Leaky Rectified Linear Unit, which allows a small slope for negative values in order to allow a small activation even with negative inputs, thus reducing the problem of dead neurons.

---> Architecture of a Neural Network <---
Training a neural network gradually adjusts the weights and biases as parameters, which can be identified in the underlying architecture of the neural network. The weights (w) and biases (b) are arranged in the order in which they are output by the respective layers or input into the subsequent layers. The first hidden layer receives the input values of the four independent variables from the original data from the input layer, which is why four columns are provided for the weights in the architecture of the neural network. These four columns represent the number of neurons in the previous layer, i.e., the input layer. The rows represent the number of neurons in the current layer, which in this example is four neurons in the first hidden layer. The four neurons not only pass their weights on to the subsequent layer, but these are also supplemented by the biases from the training process. The mathematical procedure used here is known as matrix multiplication. In the output layer, there is ultimately only one neuron, which can classify between 0 and 1 for “Versicolor” or “Virginica”. The resulting architecture of the neural network looks like this:
---> Weights <---
Weights determine the strength of the connection between neurons in adjacent layers of the network. A weight multiplies the input values before they are passed on to the next neuron (keyword: matrix multiplication). Higher weight values amplify the input, lower values weaken it.
---> Biases <---
Biases are additional values that can be used to shift the output of a neuron. This allows the neural network to learn more flexibly and be adapted to specific requirements. Example: Without a corresponding bias, a neuron could only ever have an output of 0 if the input values are also 0. The bias prevents this in order to preserve the input values for the further training process.

---> Confusion Matrix <---
A confusion matrix is a table used to evaluate the performance of a classification model. It shows how well the model predicts different classes by comparing the actual values with the predicted values. The matrix usually consists of four fields. True positives (TP): The number of correct positive predictions (the model says “positive” and it is also ‘positive’). False positives (FP): The number of incorrect positive predictions (the model says “positive”, but it is actually “negative”). True negatives (TN): The number of correct negative predictions (the model says “negative” and it is also ‘negative’). False negatives (FN): The number of incorrect negative predictions (the model says “negative,” but it is actually “positive”). Based on the trained neural network, the following confusion matrix results:
---> Accuracy <---
The accuracy of a neural network is one of the most common metrics used to measure the performance of a classification model. It indicates how often the model made the correct prediction. Accuracy is calculated by dividing the number of correct predictions (both positive and negative) by the total number of predictions. However, accuracy is only a suitable metric if none of the cases with feature values 0 or 1 are underrepresented or overrepresented.

---> Optimization <---
Finally, false negatives and false positives can be considered incorrect predictions of the AI model in the underlying data set (Download: CSV). The aim here is to identify any special features in individual cases that deviate from the patterns learned by the neural network. This may not only enable the neural network to be optimized through retraining, modified hyperparameters, or adjusted data, but also provide an understanding of the limitations that need to be taken into account when using a neural network with the given data:
---> Concluding Remarks <---
Manual optimization is possible outside of the tutorial using a programming language such as Python or MicroPython to transfer AI models to the professional context as needed. This tutorial is based on an open source framework that transparently displays all parameters and hyperparameters of a neural network, allowing AI models to be flexibly adapted and made explainable - for example, the number of neurons and layers, as well as the activation functions used, including export to a microcontroller such as the Raspberry Pi Pico (Link: AI-ANNE). With regard to the classification of irises, it should be noted that such AI models should only be understood and used as assistance systems, for example, to provide information in the event of an increased number of cases. The fact that the information provided by an AI model may not be correct was illustrated by the false positives and false negatives. Human expertise and experience cannot be replaced by the AI model.


Prof. Dr. habil. Dennis Klinkhammer
www.STATISTICAL-THINKING.de