







---> Thèmes <---
Dans ce tutoriel, un réseau neuronal peut être entraîné directement dans le navigateur. La structure et le fonctionnement d'un réseau neuronal, qui constituent la base des modèles d'IA, sont décrits, et les neurones et les couches sont présentés comme des concepts fondamentaux essentiels des réseaux neuronaux. En outre, le nombre d'époques et le taux d'apprentissage associé sont présentés comme des hyperparamètres, qui peuvent influencer considérablement le processus d'entraînement des modèles d'IA. Enfin, le processus d'entraînement du réseau neuronal peut être utilisé pour illustrer le concept des fonctions d'activation, qui déterminent comment les paramètres appris sont convertis en sorties sous forme de poids et de biais. Si ceux-ci sont identifiés de manière transparente, les modèles d'IA peuvent être adaptés et optimisés en fonction d'exigences spécifiques. La précision du modèle peut alors être évaluée à l'aide de la matrice de confusion et de la précision qui en résulte. Enfin, une compréhension des faux négatifs et des faux positifs permet une analyse cas par cas basée sur les données afin d'évaluer le processus d'apprentissage, la qualité des données utilisées et la qualité du modèle d'IA.
---> Objectifs <---
Dans l'ensemble, le tutoriel se concentre sur les concepts de base essentiels des réseaux neuronaux, une présentation simplifiée des principes mathématiques fondamentaux, l'interprétabilité des résultats qui en découle et les possibilités d'optimisation. L'objectif général du tutoriel est de fournir une explication transparente du fonctionnement des réseaux neuronaux afin de favoriser une meilleure compréhension des modèles d'IA.

---> Dataset <---
Le tutoriel est basé sur un ensemble de données (Téléchargement: CSV) permettant de classer les espèces d'iris, avec des informations sur la longueur et la largeur des sépales et des pétales. L'ensemble de données contient au total quatre variables indépendantes qui peuvent être utilisées pour classer les iris. En outre, il existe une variable dépendante qui fournit des informations sur l'espèce d'iris en question. Il s'agit donc de cas déjà connus, sur la base desquels le réseau neuronal doit apprendre les modèles (complexes) qui peuvent sous-tendre les espèces d'iris afin de les classer correctement. Cela suppose toutefois que les cas futurs présenteront des modèles similaires à ceux utilisés pour entraîner le réseau neuronal.
---> Variables <---
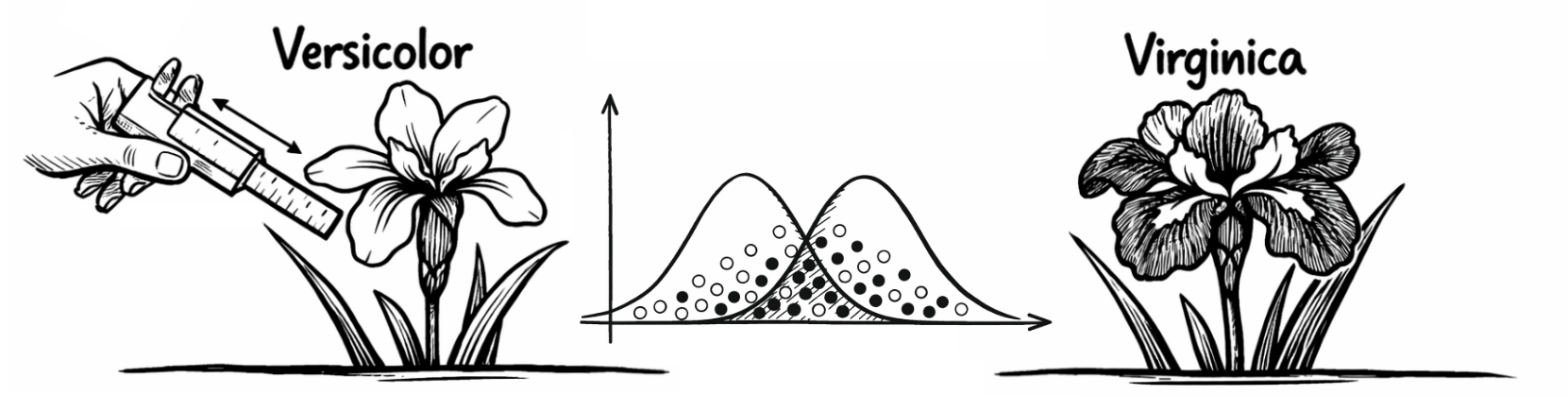
Les variables indépendantes sont : (1) la longueur du sépale (cm), (2) la largeur du sépale (cm), (3) la longueur du pétale (cm) et (4) la largeur du pétale (cm). Cependant, la similitude des variables indépendantes rend la classification difficile. La variable dépendante contient donc les caractéristiques 0 pour "Versicolor" et 1 pour "Virginica" pour les espèces d'iris sous-jacentes. Les variables sont calibrées de manière égale et ne nécessitent pas de normalisation supplémentaire.

---> Neurones <---
Les neurones d'un réseau neuronal sont des éléments de base capables de traiter des informations. Ils reçoivent des données, les traitent, puis génèrent une sortie correspondante. Les neurones peuvent être connectés à d'autres neurones, ce qui signifie que les données d'un neurone sont généralement basées sur la sortie d'un autre neurone. Le petit réseau neuronal affiché par défaut montre initialement 11 neurones sur toutes les couches, tandis que le réseau neuronal plus grand montre 17 neurones sur toutes les couches.
---> Couches <---
Les couches d'un réseau neuronal sont des groupes de neurones qui travaillent ensemble pour traiter les données d'entrée et générer conjointement une sortie. L'interaction entre la couche d'entrée, qui est la première couche du réseau neuronal pour la saisie des données, les couches cachées, qui peuvent reconnaître des modèles complexes entre la couche d'entrée et la couche de sortie, et la couche de sortie, qui est la dernière couche du réseau neuronal et qui fournit la réponse d'un modèle d'IA, est cruciale. Le petit réseau neuronal affiché par défaut est basé sur 4 couches, tandis que le réseau neuronal plus grand est basé sur 5 couches. En cliquant sur le bouton "Démarrer l'entraînement", vous entraînez le réseau neuronal et obtenez ensuite des informations sur les fonctions d'activation, les paramètres et la précision du modèle utilisés:
---> Époques <---
Les époques correspondent à des passages complets à travers toutes les données utilisées pour le processus d'apprentissage. Avec les données disponibles, cela signifie que le réseau neuronal a vu et traité chaque cas provenant des données une fois. Un réseau neuronal a généralement besoin de plusieurs époques pour reconnaître des modèles complexes. Ce paramètre, appelé hyperparamètre, doit donc être choisi avec soin. Si le réseau neuronal ne passe que par un petit nombre d'époques, il risque de ne pas avoir assez de temps pour reconnaître les modèles complexes dans les données (mot-clé: sous-ajustement). Si le réseau neuronal a trop d'époques, il peut commencer à si bien apprendre les données d'entraînement qu'il s'adapte très bien aux données du processus d'entraînement, mais cet ajustement ne peut pas être transféré à d'autres données (mot-clé: surajustement). Le réseau neuronal affiché par défaut est initialement préréglé sur 100 époques.
---> Taux d'apprentissage <---
Le taux d'apprentissage est également un hyperparamètre qui influence la rapidité ou la lenteur avec laquelle le réseau neuronal apprend de ses erreurs. Il contrôle la taille des étapes que le réseau effectue lors de l'ajustement des poids pendant le processus d'apprentissage. Un taux d'apprentissage trop élevé peut amener le modèle à ignorer la solution optimale, tandis qu'un taux d'apprentissage trop faible peut rendre l'apprentissage très lent et inefficace. Le taux d'apprentissage par défaut du réseau neuronal affiché par défaut est de 0,05 et peut être ajusté en conséquence.

---> Fonctions d'activation <---
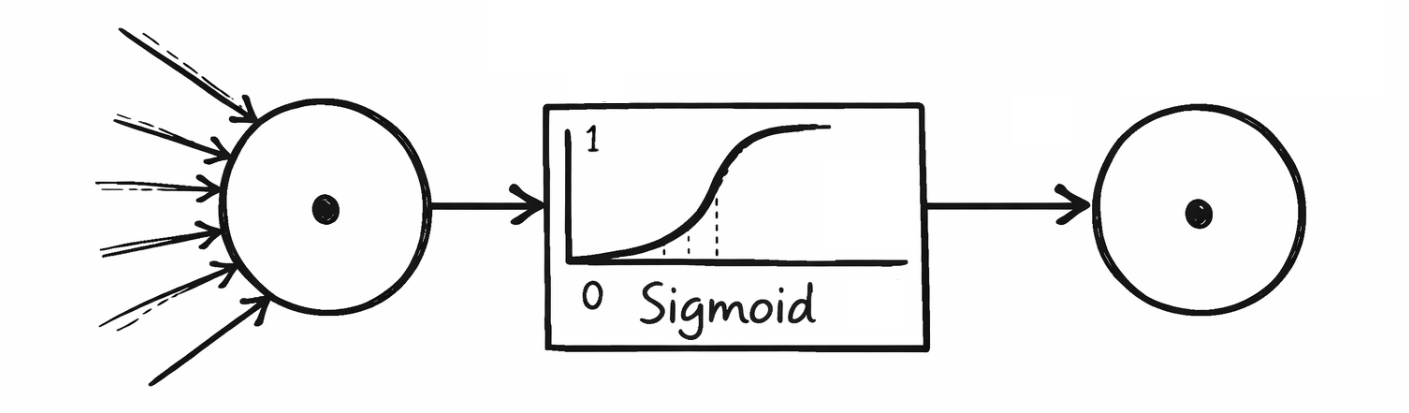
Les fonctions d'activation déterminent l'intensité avec laquelle un neurone est activé et la sortie qu'il transmet à la couche suivante. Elles permettent de filtrer les informations non pertinentes et de renforcer les modèles pertinents. Les fonctions d'activation fréquemment utilisées et stockées dans les réseaux neuronaux du tutoriel sont la fonction sigmoïde, la tangente hyperbolique, l'unité linéaire rectifiée et l'unité linéaire rectifiée à fuite. Le tableau suivant indique quelles fonctions d'activation ont été utilisées dans quelles couches:
---> Contexte Mathématique <---
La fonction Sigmoïde produit des valeurs comprises entre 0 et 1 et est souvent utilisée dans la couche de sortie des classificateurs binaires pour calculer, par exemple, la probabilité de 1 "Virginica". La Tangente Hyperbolique, quant à elle, produit des valeurs comprises entre -1 et 1 et se comporte de manière similaire à la fonction Sigmoïde, mais elle est plus symétrique et avantageuse lorsque la sortie doit être centrée. L'Unité Linéaire Rectifiée est l'une des fonctions d'activation les plus couramment utilisées et renvoie directement la valeur d'entrée si elle est supérieure à 0, sinon elle renvoie 0. Cependant, cela peut entraîner la désactivation des neurones à moyen ou long terme pendant le processus d'apprentissage (mot-clé: neurones morts). Une variante de cette fonction est l'Unité Linéaire Rectifiée Avec Fuite, qui autorise une légère pente pour les valeurs négatives afin de permettre une faible activation même avec des entrées négatives, réduisant ainsi le problème des neurones morts.

---> Architecture d'un Réseau Neuronal <---
L'entraînement d'un réseau neuronal ajuste progressivement les poids et les biais en tant que paramètres, qui peuvent être identifiés dans l'architecture sous-jacente du réseau neuronal. Les poids (w) et les biais (b) sont classés dans l'ordre dans lequel ils sont émis par les couches respectives ou entrés dans les couches suivantes. La première couche cachée reçoit les valeurs d'entrée des quatre variables indépendantes provenant des données d'origine de la couche d'entrée, c'est pourquoi quatre colonnes sont prévues pour les poids dans l'architecture du réseau neuronal. Ces quatre colonnes représentent le nombre de neurones dans la couche précédente, c'est-à-dire la couche d'entrée. Les lignes représentent le nombre de neurones dans la couche actuelle, qui dans cet exemple est de quatre neurones dans la première couche cachée. Les quatre neurones transmettent non seulement leurs poids à la couche suivante, mais ceux-ci sont également complétés par les biais issus du processus d'apprentissage. La procédure mathématique utilisée ici est connue sous le nom de multiplication matricielle. Dans la couche de sortie, il n'y a finalement qu'un seul neurone, qui peut classer entre 0 et 1 pour "Versicolor" ou "Virginica". L'architecture résultante du réseau neuronal se présente comme suit:
---> Poids <---
Les poids déterminent la force de la connexion entre les neurones dans les couches adjacentes du réseau. Un poids multiplie les valeurs d'entrée avant qu'elles ne soient transmises au neurone suivant (mot-clé : multiplication matricielle). Des valeurs de poids plus élevées amplifient l'entrée, tandis que des valeurs plus faibles l'affaiblissent.
---> Biais <---
Les biais sont des valeurs supplémentaires qui peuvent être utilisées pour modifier la sortie d'un neurone. Cela permet au réseau neuronal d'apprendre de manière plus flexible et de s'adapter à des exigences spécifiques. Exemple : sans biais correspondant, un neurone ne pourrait avoir qu'une sortie de 0 si les valeurs d'entrée sont également de 0. Le biais empêche cela afin de préserver les valeurs d'entrée pour la suite du processus d'apprentissage.

---> Confusion Matrix <---
Une matrice de confusion est un tableau utilisé pour évaluer les performances d'un modèle de classification. Elle montre la capacité du modèle à prédire différentes classes en comparant les valeurs réelles aux valeurs prédites. La matrice se compose généralement de quatre champs. True Positives (TP): nombre de prédictions positives correctes (le modèle indique "positif" et le résultat est également "positif"). False Positives (FP): nombre de prédictions positives incorrectes (le modèle indique "positif", mais le résultat est en réalité "négatif"). True Negatives (TN): nombre de prédictions négatives correctes (le modèle indique "négatif" et c'est également "négatif"). False Negatives (FN): nombre de prédictions négatives incorrectes (le modèle indique "négatif", mais c'est en réalité "positif"). Sur la base du réseau neuronal entraîné, la matrice de confusion suivante est obtenue:
---> Précision <---
La précision d'un réseau neuronal est l'un des indicateurs les plus couramment utilisés pour mesurer les performances d'un modèle de classification. Elle indique la fréquence à laquelle le modèle a fait des prédictions correctes. La précision est calculée en divisant le nombre de prédictions correctes (positives et négatives) par le nombre total de prédictions. Cependant, la précision n'est un indicateur approprié que si aucun des cas avec des valeurs de caractéristiques 0 ou 1 n'est sous-représenté ou surreprésenté.

---> Optimization <---
Enfin, les faux négatifs et les faux positifs peuvent être considérés comme des prédictions incorrectes du modèle d'IA dans l'ensemble de données sous-jacent (Téléchargement: CSV). L'objectif ici est d'identifier toute caractéristique particulière dans des cas individuels qui s'écarte des modèles appris par le réseau neuronal. Cela peut non seulement permettre d'optimiser le réseau neuronal par un réentraînement, une modification des hyperparamètres ou un ajustement des données, mais aussi de comprendre les limites à prendre en compte lors de l'utilisation d'un réseau neuronal avec les données données:
---> Concluding Remarks <---
L'optimisation manuelle est possible en dehors du tutoriel à l'aide d'un langage de programmation tel que Python ou MicroPython afin de transférer les modèles d'IA vers le contexte professionnel selon les besoins. Ce tutoriel est basé sur un cadre open source qui affiche de manière transparente tous les paramètres et hyperparamètres d'un réseau neuronal, permettant ainsi d'adapter les modèles d'IA de manière flexible et de les rendre explicables, par exemple le nombre de neurones et de couches, ainsi que les fonctions d'activation utilisées, y compris l'exportation vers un microcontrôleur tel que le Raspberry Pi Pico (Lien: AI-ANNE). En ce qui concerne la classification des iris, il convient de noter que ces modèles d'IA ne doivent être compris et utilisés que comme des systèmes d'aide, par exemple pour fournir des informations en cas d'augmentation du nombre de cas. Le fait que les informations fournies par un modèle d'IA puissent ne pas être correctes a été illustré par les faux positifs et les faux négatifs. L'expertise et l'expérience humaines ne peuvent être remplacées par le modèle d'IA.


Prof. Dr. habil. Dennis Klinkhammer
www.STATISTICAL-THINKING.de