







---> 主题 <---
在本教程中,神经网络可直接在浏览器内进行训练。作为人工智能模型的基础,神经网络的结构与运作原理在此得到阐述,并介绍了神经元以及层作为神经网络的核心基本概念。此外,还介绍了作为所谓超参数的训练轮次及相关学习率,这些参数能显著影响人工智能模型的训练过程。最后,通过神经网络的训练过程阐释激活函数的概念,该函数决定了学习参数如何以权重和偏置的形式转化为输出结果。若能清晰识别这些参数,即可针对特定需求对人工智能模型进行调整与优化。随后可通过混淆矩阵及由此得到的准确率对模型性能进行评估。通过深入理解假阴性与假阳性情况,可基于数据进行个案分析,从而评估训练过程、所用数据质量以及人工智能模型的整体质量。
---> 目标 <---
总体而言,本教程聚焦于神经网络的核心基础概念,以简化形式呈现数学原理,阐释其结果的可解释性,并探讨优化可能性。教程的总体目标是清晰阐明神经网络的工作原理,从而促进对人工智能模型的深入理解。

---> 数据集 <---
本教程基于一个用于鸢尾花种类分类的数据集(下载:CSV),其中包含萼片与花瓣的长度及宽度信息。该数据集包含四个独立变量,可用于鸢尾花的分类,此外还包含一个因变量,用于指示对应的鸢尾花种类。因此,这些数据属于已知案例,神经网络需在此基础上学习潜在的(复杂)模式,以便对鸢尾花种类进行正确分类。但这要求未来案例呈现出与用于训练神经网络的数据相似的模式特征。
---> 变量 <---
自变量包括:(1) 萼片长度(厘米),(2) 萼片宽度(厘米),(3) 花瓣长度(厘米),(4) 花瓣宽度(厘米)。然而,自变量之间的相似性使得分类变得困难。因此,因变量采用二进制编码:0 表示 “Versicolor”,1 表示 “Virginica”。所有变量均采用相同尺度进行缩放,无需额外的标准化处理。

---> 神经元 <---
神经网络中的神经元是能够处理信息的基本单元。它们接收输入信号,进行处理后产生相应的输出信号。神经元之间可以相互连接,这意味着一个神经元的输入通常基于另一个神经元的输出。默认显示的小型神经网络最初在所有层中共包含11个神经元,而大型神经网络则在所有层中共包含17个神经元。
---> 层 <---
神经网络中的层是由神经元组成的集合,它们协同处理输入数据并共同生成输出。其中,输入层作为神经网络接收数据的第一层,隐藏层位于输入层与输出层之间,能够识别复杂模式,而输出层作为神经网络的最后一层,输出人工智能模型的结果,这些层之间的协同作用至关重要。默认显示的小型神经网络基于4层结构,而大型神经网络则基于5层结构。点击“开始训练”按钮将对神经网络进行训练,随后可查看所使用的激活函数、参数及模型准确率:
---> 纪元 <---
训练周期是指对训练过程中使用的全部数据进行完整遍历的过程。对于当前数据集而言,这意味着神经网络已对每个数据样本进行过一次识别与处理。神经网络通常需要多个训练周期才能识别复杂模式。因此必须谨慎选择这一所谓的超参数。若神经网络仅运行较少数量的训练周期,可能因时间不足而无法识别数据中的复杂模式(关键词:欠拟合)。若神经网络经历过多训练周期,则可能对训练数据产生过度学习,使其高度拟合训练过程中的数据,但这种拟合无法迁移到其他数据上(关键词:过拟合)。默认显示的神经网络初始预设训练周期为100次。
---> 学习率 <---
学习率同样属于超参数范畴,它决定了神经网络从错误中学习的速度快慢。该参数控制着网络在训练过程中调整权重时所采取的步长大小。过高的学习率可能导致模型错过最优解,而过低的学习率则会使训练过程变得极其缓慢且效率低下。默认情况下,所展示神经网络的学习率设定为0.05,用户可根据实际需求进行相应调整。

---> 激活函数 <---
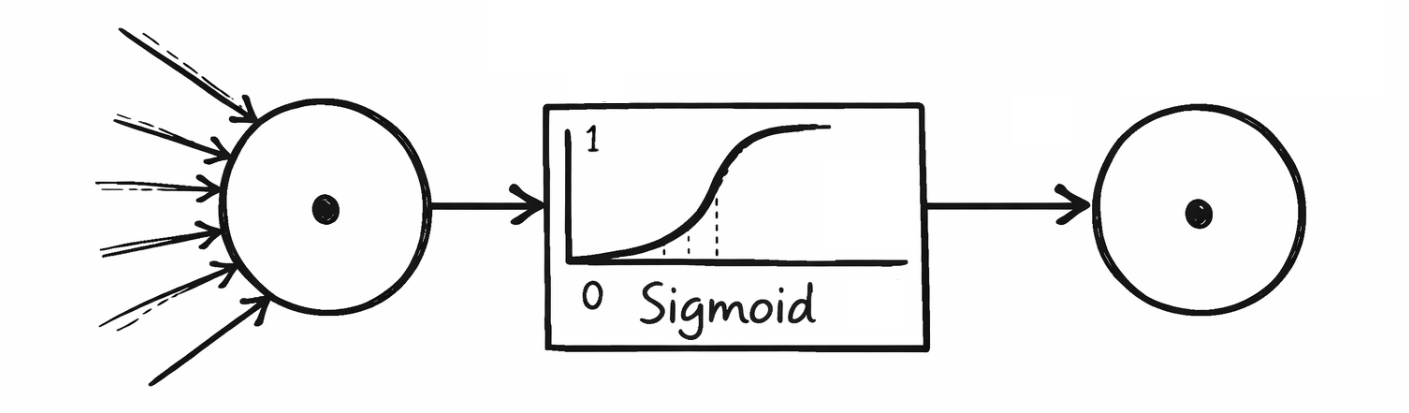
激活函数决定神经元被激活的强度以及其传递给下一层的输出值。它们有助于过滤无关信息并强化相关模式。教程中神经网络常用的激活函数包括:S形函数、双曲正切函数、整流线性单元(ReLU)和漏泄整流线性单元(Leaky ReLU)。下表展示了各层使用的激活函数:
---> 数学背景 <---
S形函数输出值范围为(0, 1),常用于二元分类器的输出层,例如计算 “Virginica” 为1的概率。双曲正切函数的输出值范围为(-1, 1),其行为与S形函数相似,但具有更强的对称性,在需要输出值居中的场景下更具优势。Rectified Linear Unit是最常用的激活函数之一,当输入值大于0时直接返回输入值,否则输出0。但这可能导致训练过程中神经元在中长期内被关闭(关键词:死神经元)。其一种变体是Leaky Rectified Linear Unit,它允许负值具有一个很小的斜率,即使在负输入情况下也能产生微弱激活,从而缓解死神经元问题。

---> 神经网络的架构 <---
训练神经网络时,会逐步调整权重和偏置作为参数,这些参数可在神经网络的基础架构中进行识别。权重 (w) 和偏置 (b)按照各层输出的顺序或输入到后续层的顺序进行排列。第一隐藏层从输入层接收原始数据中四个独立变量的输入值,因此在神经网络架构中为权重设置了四列。这四列代表前一层神经元的数量,即输入层。行代表当前层神经元的数量,在本示例中,第一隐藏层包含四个神经元。这四个神经元不仅将其权重传递至后续层,同时还加入了训练过程中得到的偏置。此处采用的数学运算称为矩阵乘法。输出层最终仅包含一个神经元,其输出值在 0 和 1 之间,用于区分 “Versicolor” 或 “Virginica”。由此得到的神经网络架构如下所示:
---> 重量 <---
权重决定了网络相邻层神经元之间连接的强度。权重值会在对输入值进行乘法运算后再传递至下一神经元(关键词:矩阵乘法)。权重值越高,输入信号被放大;权重值越低,输入信号则被削弱。
---> 偏见 <---
偏置是可用于偏移神经元输出结果的附加值。这使得神经网络能够更加灵活地学习并适应特定需求。例如:若无对应偏置,当输入值均为0时,神经元输出将永远为0。偏置的存在避免了这种情况,从而为后续训练过程保留输入值。

---> 混淆矩阵 <---
混淆矩阵是一种表格,用于评估分类模型的性能。它通过比较实际值与预测值,展示模型对不同类别的预测效果。该矩阵通常包含四个字段。True Positive(TP):正确预测阳性的数量(模型判定为“阳性”且实际为“阳性”)。False Positive(FP):错误预测阳性的数量(模型判定为“阳性”,但实际为“阴性”)。True Negative(TN):正确预测为阴性的数量(模型判定为“阴性”,实际也为“阴性”)。False Negative(FN):错误预测为阴性的数量(模型判定为“阴性”,但实际为“阳性”)。基于训练后的神经网络,得到如下混淆矩阵:
---> 准确性 <---
神经网络的准确率是最常用的指标之一,用于衡量分类模型的性能,它反映了模型做出正确预测的频率。准确率通过将正确预测数(包括正例和负例)除以总预测数计算得出。然而,准确率仅在特征值为0或1的案例未出现严重偏倚(即未被低估或高估)时才适用。

---> 优化 <---
最后,假阴性与假阳性可视为AI模型的错误预测,这些预测出现在基础数据集中(下载:CSV)。此处的目标是识别个别案例中的特殊特征,这些特征偏离了神经网络所学习的模式。这不仅可以通过重新训练、调整超参数或修改数据来优化神经网络,还能帮助理解在给定数据条件下使用神经网络时需要考虑的局限性:
---> 结语 <---
在教程之外,用户可通过 Python 或 MicroPython 等编程语言进行手动优化,以便将 AI 模型按需引入专业应用场景。本教程基于开源框架,可透明展示神经网络的所有参数与超参数,从而实现 AI 模型的灵活调整与可解释性——例如神经元数量、层数以及所使用的激活函数,并支持导出至微控制器,如 Raspberry Pi Pico(链接:AI-ANNE)。在鸢尾花分类的背景下需要强调的是,此类 AI 模型仅应作为辅助系统 来理解和使用,例如在案例数量增加时提供参考信息。模型所提供的提示并不一定是正确的,这一点已通过假阳性与假阴性结果得以说明。人类的专业知识与经验无法被 AI 模型所取代。


Prof. Dr. habil. Dennis Klinkhammer
www.STATISTICAL-THINKING.de